|
Julie Ellis (New Zealand) has authored two of our favourite mathematical stories, 'What's Your Angle, Pythagoras?' (2004) and 'Pythagoras and the Ratios' (2010), both are illustrated by Phyllis Hornung Peacock and published by Charlesbridge. To learn more about these stories, and find out where you can purchase them, simply click on their covers below. We hope you enjoy reading Julie sharing her experience of working on these incredible mathematical story projects with you! |
|
First thing first, can you tell us three interesting/weird facts about you :-)
I grew up with 3 brothers in a small town in New Zealand. There were no shopping malls or computers, so we spent lots of time playing outside. I learnt to do some weird things such as blow a shepherd’s whistle, touch my nose with my tongue, and ski using a snow scooter. How would you describe your relationship with mathematics and mathematics learning when you were younger? And now? When I was at school, I hated mathematics. I didn’t understand a lot of it, and I used to panic at math time. Now, I don’t panic so much, because I know my brain is a literary brain rather than a mathematics brain. I try to view math equations as logic puzzles. "I wrote the ‘What’s Your Angle Pythagoras?’ when my 9-year-old daughter was struggling to learn the Pythagorean theorem: the square of the hypotenuse is equal to the sum of the squares of the other two sides. She didn’t understand how this could be useful in everyday life, so I found some real life examples and presented them in a story." What inspired you to write picturebooks with a mathematical focus for young children? I wrote the ‘What’s Your Angle, Pythagoras?’ when my 9-year-old daughter was struggling to learn the Pythagorean theorem: the square of the hypotenuse is equal to the sum of the squares of the other two sides. She didn’t understand how this could be useful in everyday life, so I found some real life examples and presented them in a story. I wrote ‘Pythagoras and the Ratios’ because when I was researching the Pythagorean theorem, I read about Pythagoras’s musical discoveries (tuning and scaling musical notes). I couldn’t fit both Pythagorean theorem and Pythagorean tuning into one book. Why do you prefer creating mathematical picturebooks with a storyline to, say, non-fiction mathematics concept books? Children like to read about other children. As my first two math books were about the Pythagorean theorem, I thought it would be more relatable for the audience if I wrote them from the point of view of the child Pythagoras. Also, as a child who loved reading but found math stressful, picture books appeal to me as a fun, non-threatening way to transmit information. What were some of the key stages that you went through in creating your mathematical picturebooks? First, I found examples of when the Pythagorean theorem and Pythagorean tuning are useful in real life, and then I wrote the stories around the examples. To make the stories interesting, I wrote them both from the point of view of Pythagoras when he was a boy. However, I had no idea what the first book would look like because my publisher chose the illustrator after the script had been accepted for publication. Which of these stages did you find most challenging? Similarly, which do you find most satisfying? The most challenging part was choosing which examples to use, and trying to explain them simply. It was very satisfying when I finally managed to explain things clearly, for example the way Pythagoras tuned his cousin’s lyres using rock weights. Did you find it hard to come up with a storyline / context to embed your chosen mathematical concept in? Where did you draw inspirations from? The storyline was easy once I decided to tell it from the point of view of Pythagoras as a curious boy. I just had to make sure I paced the story so that there were enough smaller problems and solutions to fill a 32 page book. Some mathematical story authors prefer to have a context and setting as close to children’s real-world experience as much as possible. Others prefer fantasy. In the context of maths stories, what is your preference, and why? I like to base my stories in the real-world as they seem more believable to me. I wrote about Pythagoras travelling to Egypt with his father when he was a boy, as according to my research that probably happened in real life. On average, how long did it take you to work on each of these books? I had to think about and plan my examples carefully and that took about 3 months. It only took a few days to write the story outline, but then it had to be edited to make it perfect. Across the sector, it is quite common for authors not to have any say in the illustration process at all. Many authors never even have any direct contacts with their book’s illustrators. What has been your experience on this? Would you prefer authors to be more involved in the illustration process? I am not an artist, however as I’m writing, I imagine what I would like the illustrations to show. After each page, I wrote a few ‘illustrators guidelines’ so that the illustrator could understand my vision, but of course the illustrator had her own ideas too. I felt nervous waiting to see the illustrations as they are so important to the visual appeal of the book. I was really pleased when I saw the finished books as the illustrator Phyllis Hornung Peacock did a brilliant job of portraying the landscape, buildings and people of ancient Greece. How do you know whether the language used in your stories is age-appropriate for your target children? I read lots of stories for the age group I am writing for. I also read my stories aloud to children and ask for their feedback. There is normally a book word count, rather than a page word count, but this is only a guide. I edit every single word in my stories. Is it the best word I could use? Does each sentence flow when read aloud? Are there any unnecessary words or sentences that should be removed? On reflection, how would you comment on the diversity of the characters in your mathematical stories? Would you have done anything differently in terms of the diversity of the characters? Because Pythagoras was a real man, I had to have a boy as my main character. My first book was about Pythagoras and his parents, but in the second book I added more children, both girls and boys. At first the girls and boys were in competition with each other, but then they decided to co-operate and play their instruments together. |
Do you think the use of storytelling in mathematics learning is only applicable to young children? Do you think this could be used in maths lessons in secondary schools too?
A picture book is simply a ‘format’. There are many adult picture books that are amusing to read. To condense a mathematical concept into easily understood language, with a word limit of around 2,000 words, and spread across 32 pages, in an exciting and page turning way, is a challenge for both those who like mathematics and those who like literacy. It is a chance for students to use their imaginations and creativity in a mathematical setting. It is also a great way for students to share their understanding of concepts with their peers. What do you think are some of the key benefits of helping children to develop their mathematical understanding by encouraging them to read maths picturebooks? As someone who struggles with math, but enjoys reading, I love that math can be taught though picture books. Math makes more sense to me when presented in this non-threatening format. Also, by putting math concepts into picture books, numeracy and literacy are being integrated, which connects the subjects, and helps students with literary minds understand math. Of course, picture books are made to be re-read, so if a reader doesn’t understand the math the first time they read the book, they can re-read it numerous times, until it makes sense to them. What do you think are some of the key benefits of helping children to develop their mathematical understanding by encouraging them to produce their own maths picturebooks? When writing about a math concept, not only do you have to understand the concept, but you must be able to explain it in very simple terms. If you can explain a math concept in simple terms, then you really understand it, and will remember it well. “A great way to consolidate learning is to have children explain a concept to someone else. Ask children to verbally tell you about a math concept that they find interesting. Encourage them to explain this concept with as many different examples as possible [...].” For teachers and parents who want to encourage their children to create their own maths picturebooks at school or at home, but are not sure how to guide them through the process, what would be your advice? A great way to consolidate learning is to have children explain a concept to someone else. Ask children to verbally tell you about a math concept that they find interesting. Encourage them to explain this concept with as many different examples as possible, and to write down their examples. In ‘What’s Your Angle, Pythagoras’, I showed multiple uses of the Pythagorean theorem. Picture books are traditionally 32 pages long, however younger children might find it easier to write a book that is 8, 12, or 24 pages. Once they have selected a math concept with examples, and a book length, have them plan their story outline in a storyboard format. Their story needs a beginning, a middle and an end, and enough interest to keep the audience wanting to read. Warn the children that writing a book involves not only planning, but revision and rewriting of drafts based on audience feedback. It is a slow process but it should also be exiting and enjoyable, so keep your feedback positive. For teachers and parents who want to have a go at having their own maths picturebook published by a publisher, what would be your advice? Do your research. Has this concept already been written about? What makes your story unique? Why would children want to read it? Why would a publisher want to publish it? Your book needs to stand out from the other scripts. It must be unique, marketable, mathematically accurate, and enjoyable to read. Read and analyze picture books at the level you want to write, for example, kindergarten, elementary, middle school or high school. Choose an appropriate mathematical concept and think about that concept in depth. What is the point of the concept? What would happen if the concept were misinterpreted? How is the concept useful and relevant? Now plan a book of 32 pages, ensuring that each alternate page has a small problem or dilemma that will encourage the reader to want to read the page. Once your book is completed, seek audience feedback and revise your text until it is as perfect as possible. Finally, send your manuscript to a publisher of children’s picture books, and if it is rejected, take on board any feedback and then send it to another publisher. Do you have any favourite mathematical story author(s)? If so, which one, and which aspects of their works do you particularly like? I particularly like Cindy Neuschwander’s Sir Cumference series of books, as the medieval time period is interesting and her explanations of mathematical concepts are fun. Can your fans expect to read any more mathematical stories from you in the future? It is possible there will be one more Pythagoras book. “The MathsThroughStories.org website is a unique and valuable resource. Not only does it provide a comprehensive list of mathematical stories, and teaching ideas, it backs this information up with research.” What do you think of the research that we do and the resources that we provide to teachers and parents on our MathsThroughStories.org website? The MathsThroughStories.org website is a unique and valuable resource. Not only does it provide a comprehensive list of mathematical stories, and teaching ideas, it backs this information up with research. As a former teacher, I understand the importance of research. New teaching ideas must be evidence-based if they are going to be used in schools. The academic expertise and diversity of nationalities of the research co-investigators will ensure that MathsThroughStories.org provides quality international perspectives on teaching math through literature. |
Illustrations copyright © 2004 by Phyllis Hornung Peacock from What's Young Angle, Pythagoras? by Julie Ellis. Charlesbridge. All Rights Reserved.
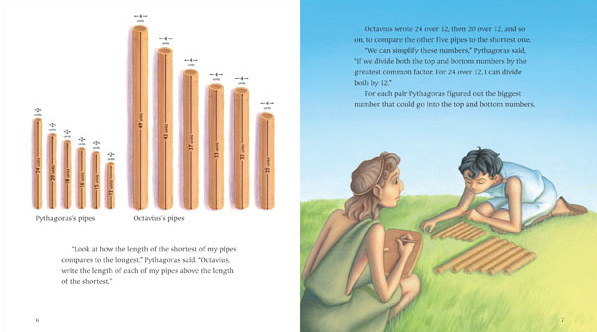
Illustrations copyright © 2010 by Phyllis Hornung Peacock from Pythagoras and the Ratios by Julie Ellis. Charlesbridge. All Rights Reserved.
Illustrations copyright © 2010 by Phyllis Hornung Peacock from Pythagoras and the Ratios by Julie Ellis. Charlesbridge. All Rights Reserved.